हेल्लो दोस्तों आज के इस पोस्ट में आपको Cyclic Redundancy checks in hindi के बारे में बताया गया है की इसे कैसे प्रयोग करते है तो चलिए शुरू करते है
Cyclic Redundancy Checks-CRC
यह साइक्लिक रिडयन्डेन्सी चैक्स (Cyclic Redundancy Checks) अत्यन्त शक्तिशाली और कार्यान्वित करने में सरल तकनीक है। चैकसम स्कीम (Checksum Scheme), जोकि Addition पर आधारित है, से भिन्न CRC बायनरी विभाजन (Binary Division) पर आधारित है।
CRC में, रिड्यून्डेन्ट बिट्स का एक अनुक्रम (A Sequence of Redundant Bits), जिसे साइक्लिक रिड्यन्डेन्सी चैक बिटस (Cyclic Redundancy Check Bits) कहा जाता है, को डेटा यूनिट (Data Unit) के अन्त में इस प्रकार संलग्न किया जाता है कि परिणाम के रूप में प्राप्त डेटा यूनिट (Data Unit) एक सेकण्ड, जोकि पूर्वनिर्धारित बाइनरी नम्बर (Binary Number) होता है से पर्णत: विभाजित हो जाए।
रिसीवर (Receiver) पर आने वाली डेटा यूनिट (Data Unit) को उसी नम्बर से विभाजित किया जाता है। यदि इसके परिणाम में कोई शेषफल प्राप्त नहीं होता है, तो डेटा यूनिट (Data Unit) को सही माना जाता है और इसलिए इसे स्वीकार कर लिया जाता है। परिणाम में शेषफल प्राप्त होता है,
तो इसका तात्पर्य है कि डेटा यनिट (Data unit) ट्रांजीशन(transition) के दौरान क्षतिग्रस्त हो गई है, अतः इसे अस्वीकार कर दिया जाता है। इस व्यापक तकनीक Unit), ट्रान्जीशन (Transition) के दौरान क्षात (Generalized Technique) की व्याख्या निम्नानुसार की जा सकती है
इसे भी जाने –
- what is checksum in hindi-चेकसम क्या होता है ?
- Two dimensional parity check in hindi-टू डायमेंशनल क्या है?
- what is Error detecting code in hindi-एरर डेतेक्टिंग कोड क्या है?
- Error detection and correction in hindi-एरर डिटेक्शन और करेक्शन क्या है?
- what is satellite network in hindi-सॅटॅलाइट नेटवर्क क्या है?
यदि एक k बिट का मेसेज transmit किया जाना है तो ट्रांसमीटर एक r बिट की sequence जिसे (frame check sequency)(FSC) के नाम से जाना जाता है
जेनेटर (Generate) करता है. इस प्रकार वास्तव में बिटस टान्समिट होते हैं। अब । शून्यों (Zeros) संलग्न मल नंबर (Original Number) को पूर्वनिर्धारित नम्बर (Predetermined Number) a से भाग दिया जाता है। यह नम्बर r+ 1 लम्बाई का होता है, जिसे गुणकों के बहपदीय (Coefficients of Polynomial) के रूप में विचारा जा सकता है,
को जेनरेटर पॉलीनॉमिअल (Generator Polynomial) कहते हैं। इस भाग प्रक्रिया का शेषफल (Remainder) r बिट FCS जेनरेट (Generate) करता है। इस पैकेट को प्राप्त करने पर रिसीवर (Receiver) k+7 बिट फ्रेम को उसी पूर्वनिर्धारित नम्बर से भाग देता है और यदि शेषफल शून्य प्राप्त होता है,
तो यह माना जा सकता है कि ट्रान्समिशन (Transmission) के दौरान कोई त्रुटि उपस्थित नहीं हुई है। सेन्डर (Sender) और रिसीवर (Receiver) पर इस प्रक्रिया को निम्नांकित डायग्राम में दर्शाया गया है
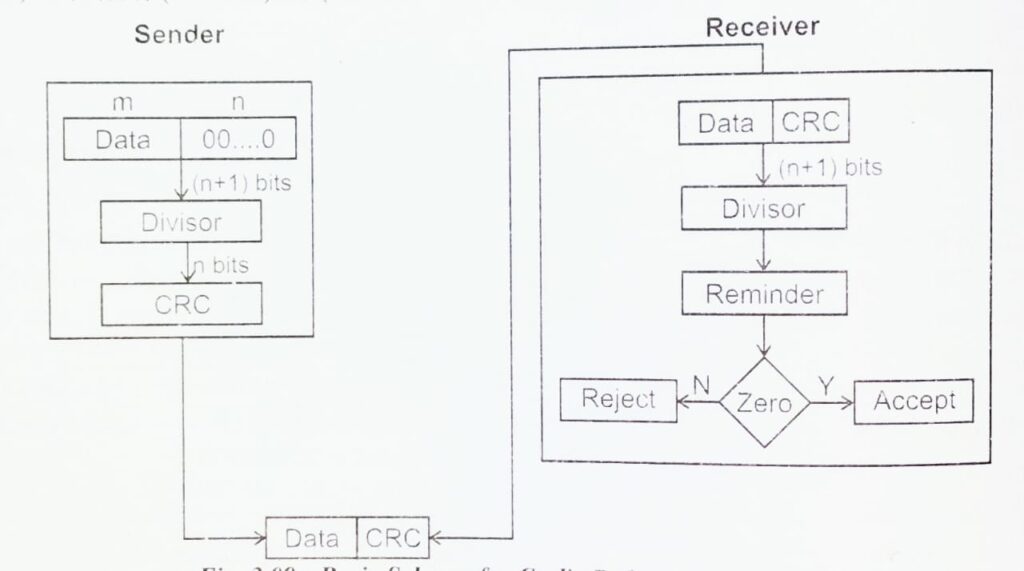
एक प्रतिदर्श 4 बिट नम्बर को जेनरेटर पॉलीनॉमिअल के गुणक x3 + x +1. जोकि 1011 के से माड्यूलो-2 अर्थमेटिक (Modulo-2 Arithmetic) का प्रयोग करके भाग देने की इस गणितीय क्रियान्वित प्रक्रिया को निम्नांकित डायग्राम में दशाया गया है
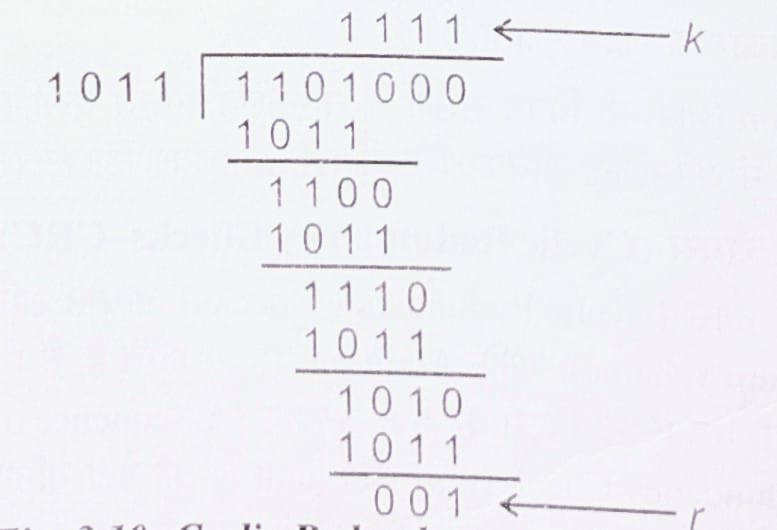
माड्यूलो -2 अर्थमेटिक (Modulo-2 Arithmetic) एक बिना किसी कैरी ओवर(Carry Over) के बाइनरी एडीशन प्रोसेस है जो मात्र Exclusive-OR Operation है। एक ऐसी परिस्थिति पर विचार करते है। है जिसमे k = 1101। अतः हमें 1101000 अर्थात् k के साथ तीन शून्य संलग्न हैं. को 1011 से भाग देना है जो की शेषफल के रूप में r = 001 प्रदान करता है
इस प्रकार वास्तव में कम्यूनिकेशन चैनल द्वारा transmit होने वाला बिट फ्रेम (k + r) = 1101001 है यदि receiver द्वारा प्राप्त किए गए नम्बर अर्थात् 1101001 को उसी जेनरेटर पोलिंनोमिअल 1011 से भाग दिया गया है तो प्राप्त होने वाला शेषफल 000 होगा और यह माना जा सकता है कि डेटा त्रुटि रहित है।
एरर करेक्शन कोड्स (Error Correction Codes )
अभी तक हमने एरर (Error) को डिटेक्ट (Detect) करने की तकनीकों की चर्चा की है, ये तकनीक एरर (Error) को करेक्ट (Correct) नहीं करती हैं। एरर करेक्शन (Error Correction) निम्नांकित दो प्रकार से की जा सकती है
(1) जब एरर (Error) को खोजा जाए, तब रिसीवर (Receiver) समस्त डेटा यूनिट (Data Unit) को रिट्रान्समिट (Retransmit) कर सके। इसे बैकवर्ड एरर करेक्शन (Backward Error Correction) कहा जाता है।
(2) जब एरर (Error) को खोजा जाए, तब रिसीवर एरर करेक्शन कोड (Error Correction Code) का प्रयोग कर सके,जोकि विशेष एरसे (Errors) को स्वतः ही करेक्ट (Correct) कर सके। इसे फॉरवर्ड एरर करेक्शन (Forward Error Correction) कहा जाता है।
सैद्धान्तिक रूप से यह सम्भव है कि किसी भी संख्या में प्राप्त हुई एरर्स (Errors) को स्वतः ही करेक्ट (Correct) किया जा सके। एरर करेक्शन कोड (Error Correction Code), एरर डिटेक्शन कोड (Error Detection Code) की अपेक्षा अधिक परिष्कृत (Sophisticated) होते हैं
और इनके लिए अधिक रिड्यून्डेन्ट बिट्स (Redundant Bits) की आवश्यकता होती है। मल्टीपल-बिट (Multiple-Bit) अथवा बर्स्ट एरर (Burst Error) को करेक्ट (Correct) करने के लिए आवश्यक बिट्स (Bits) की संख्या की आवश्यकता अत्यन्त उच्च होती है और अधिकांश परिस्थितियों में ऐसा करना अप्रभावशाली होता है। इस कारण अधिकांश एरर करेक्शन (Error Correction) एक, दो अथवा अधिकतम तीन बिट एरर्स (Bit Errors) तक सीमित होती हैं।
reference-https://www.geeksforgeeks.org/modulo-2-binary-division/
निवेदन:-आप सभी छात्र –छात्रों से निवेदन है की अगर आपको ये Topic(Cyclic Redundancy checks in hindi) अच्छा लगा हो तो कृपया आप( Cyclic Redundancy checks in hindi ) इस वेबसाइट के बारे में अपने दोस्तों को जरुर बताये अगर कोई topic से संबधित प्रश्न हो तो कमेंट्स(comments) आपके लिए ही बना है और किसी Subject(Cyclic Redundancy checks in hindi)